Bayesian statistics and modelling
Bayesian statistics is an approach to data analysis based on Bayes’ theorem, where available knowledge about parameters in a statistical model is updated with the information in observed data. The background knowledge is expressed as a prior distribution and combined with observational data in the form of a likelihood function to determine the posterior distribution. The posterior can also be used for making predictions about future events. This Primer describes the stages involved in Bayesian analysis, from specifying the prior and data models to deriving inference, model checking and refinement. We discuss the importance of prior and posterior predictive checking, selecting a proper technique for sampling from a posterior distribution, variational inference and variable selection. Examples of successful applications of Bayesian analysis across various research fields are provided, including in social sciences, ecology, genetics, medicine and more. We propose strategies for reproducibility and reporting standards, outlining an updated WAMBS (when to Worry and how to Avoid the Misuse of Bayesian Statistics) checklist. Finally, we outline the impact of Bayesian analysis on artificial intelligence, a major goal in the next decade.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
cancel any time
Subscribe to this journal
Receive 1 digital issues and online access to articles
133,45 € per year
only 133,45 € per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout
Similar content being viewed by others
Bayesian Analysis Reporting Guidelines
Article Open access 16 August 2021
A new unit distribution: properties, estimation, and regression analysis
Article Open access 27 March 2024
Simple nested Bayesian hypothesis testing for meta-analysis, Cox, Poisson and logistic regression models
Article Open access 23 March 2023
Change history
References
- Bayes, M. & Price, M. LII. An essay towards solving a problem in the doctrine of chances. By the late Rev. Mr. Bayes, F. R. S. communicated by Mr. Price, in a letter to John Canton, A. M. F. R. S. Philos. Trans. R Soc. Lond. B Biol. Sci.53, 370–418 (1997). ADSMATHGoogle Scholar
- Laplace, P. S. Essai Philosophique sur les Probabilities (Courcier, 1814).
- König, C. & van de Schoot, R. Bayesian statistics in educational research: a look at the current state of affairs. Educ. Rev.https://doi.org/10.1080/00131911.2017.1350636 (2017). ArticleGoogle Scholar
- van de Schoot, R., Winter, S., Zondervan-Zwijnenburg, M., Ryan, O. & Depaoli, S. A systematic review of Bayesian applications in psychology: the last 25 years. Psychol. Methods22, 217–239 (2017). Google Scholar
- Ashby, D. Bayesian statistics in medicine: a 25 year review. Stat. Med.25, 3589–3631 (2006). MathSciNetGoogle Scholar
- Rietbergen, C., Debray, T. P. A., Klugkist, I., Janssen, K. J. M. & Moons, K. G. M. Reporting of Bayesian analysis in epidemiologic research should become more transparent. J. Clin. Epidemiol.https://doi.org/10.1016/j.jclinepi.2017.04.008 (2017). ArticleGoogle Scholar
- Spiegelhalter, D. J., Myles, J. P., Jones, D. R. & Abrams, K. R. Bayesian methods in health technology assessment: a review. Health Technol. Assess.https://doi.org/10.3310/hta4380 (2000). ArticleGoogle Scholar
- Kruschke, J. K., Aguinis, H. & Joo, H. The time has come: Bayesian methods for data analysis in the organizational sciences. Organ. Res. Methods15, 722–752 (2012). Google Scholar
- Smid, S. C., McNeish, D., Miočević, M. & van de Schoot, R. Bayesian versus frequentist estimation for structural equation models in small sample contexts: a systematic review. Struct. Equ. Modeling27, 131–161 (2019). MathSciNetGoogle Scholar
- Rupp, A. A., Dey, D. K. & Zumbo, B. D. To Bayes or not to Bayes, from whether to when: applications of Bayesian methodology to modeling. Struct. Equ. Modeling11, 424–451 (2004). MathSciNetGoogle Scholar
- van de Schoot, R., Yerkes, M. A., Mouw, J. M. & Sonneveld, H. What took them so long? Explaining PhD delays among doctoral candidates. PloS ONE8, e68839 (2013). ADSGoogle Scholar
- van de Schoot, R. Online stats training. Zenodohttps://zenodo.org/communities/stats_training (2020).
- Heo, I. & van de Schoot, R. Tutorial: advanced Bayesian regression in JASP. Zenodohttps://doi.org/10.5281/zenodo.3991325 (2020). ArticleGoogle Scholar
- O’Hagan, A. et al. Uncertain Judgements: Eliciting Experts’ Probabilities (Wiley, 2006). This book presents a great collection of information with respect to prior elicitation, and includes elicitation techniques, summarizes potential pitfalls and describes examples across a wide variety of disciplines.
- Howard, G. S., Maxwell, S. E. & Fleming, K. J. The proof of the pudding: an illustration of the relative strengths of null hypothesis, meta-analysis, and Bayesian analysis. Psychol. Methods5, 315–332 (2000). Google Scholar
- Veen, D., Stoel, D., Zondervan-Zwijnenburg, M. & van de Schoot, R. Proposal for a five-step method to elicit expert judgement. Front. Psychol.8, 2110 (2017). Google Scholar
- Johnson, S. R., Tomlinson, G. A., Hawker, G. A., Granton, J. T. & Feldman, B. M. Methods to elicit beliefs for Bayesian priors: a systematic review. J. Clin. Epidemiol.63, 355–369 (2010). Google Scholar
- Morris, D. E., Oakley, J. E. & Crowe, J. A. A web-based tool for eliciting probability distributions from experts. Environ. Model. Softw.https://doi.org/10.1016/j.envsoft.2013.10.010 (2014). ArticleGoogle Scholar
- Garthwaite, P. H., Al-Awadhi, S. A., Elfadaly, F. G. & Jenkinson, D. J. Prior distribution elicitation for generalized linear and piecewise-linear models. J. Appl. Stat.40, 59–75 (2013). MathSciNetMATHGoogle Scholar
- Elfadaly, F. G. & Garthwaite, P. H. Eliciting Dirichlet and Gaussian copula prior distributions for multinomial models. Stat. Comput.27, 449–467 (2017). MathSciNetMATHGoogle Scholar
- Veen, D., Egberts, M. R., van Loey, N. E. E. & van de Schoot, R. Expert elicitation for latent growth curve models: the case of posttraumatic stress symptoms development in children with burn injuries. Front. Psychol.11, 1197 (2020). Google Scholar
- Runge, A. K., Scherbaum, F., Curtis, A. & Riggelsen, C. An interactive tool for the elicitation of subjective probabilities in probabilistic seismic-hazard analysis. Bull. Seismol. Soc. Am.103, 2862–2874 (2013). Google Scholar
- Zondervan-Zwijnenburg, M., van de Schoot-Hubeek, W., Lek, K., Hoijtink, H. & van de Schoot, R. Application and evaluation of an expert judgment elicitation procedure for correlations. Front. Psychol.https://doi.org/10.3389/fpsyg.2017.00090 (2017). ArticleGoogle Scholar
- Cooke, R. M. & Goossens, L. H. J. TU Delft expert judgment data base. Reliab. Eng. Syst. Saf.93, 657–674 (2008). Google Scholar
- Hanea, A. M., Nane, G. F., Bedford, T. & French, S. Expert Judgment in Risk and Decision Analysis (Springer, 2020).
- Dias, L. C., Morton, A. & Quigley, J. Elicitation (Springer, 2018).
- Ibrahim, J. G., Chen, M. H., Gwon, Y. & Chen, F. The power prior: theory and applications. Stat. Med.34, 3724–3749 (2015). MathSciNetGoogle Scholar
- Rietbergen, C., Klugkist, I., Janssen, K. J., Moons, K. G. & Hoijtink, H. J. Incorporation of historical data in the analysis of randomized therapeutic trials. Contemp. Clin. Trials32, 848–855 (2011). Google Scholar
- van de Schoot, R. et al. Bayesian PTSD-trajectory analysis with informed priors based on a systematic literature search and expert elicitation. Multivariate Behav. Res.53, 267–291 (2018). Google Scholar
- Berger, J. The case for objective Bayesian analysis. Bayesian Anal.1, 385–402 (2006). This discussion of objective Bayesian analysis includes criticisms of the approach and a personal perspective on the debate on the value of objective Bayesian versus subjective Bayesian analysis. MathSciNetMATHGoogle Scholar
- Brown, L. D. In-season prediction of batting averages: a field test of empirical Bayes and Bayes methodologies. Ann. Appl. Stat.https://doi.org/10.1214/07-AOAS138 (2008). ArticleMathSciNetMATHGoogle Scholar
- Candel, M. J. & Winkens, B. Performance of empirical Bayes estimators of level-2 random parameters in multilevel analysis: a Monte Carlo study for longitudinal designs. J. Educ. Behav. Stat.28, 169–194 (2003). Google Scholar
- van der Linden, W. J. Using response times for item selection in adaptive testing. J. Educ. Behav. Stat.33, 5–20 (2008). Google Scholar
- Darnieder, W. F. Bayesian Methods for Data-Dependent Priors (The Ohio State Univ., 2011).
- Richardson, S. & Green, P. J. On Bayesian analysis of mixtures with an unknown number of components (with discussion). J. R. Stat. Soc. Series B59, 731–792 (1997). MATHGoogle Scholar
- Wasserman, L. Asymptotic inference for mixture models by using data-dependent priors. J. R. Stat. Soc. Series B62, 159–180 (2000). MathSciNetMATHGoogle Scholar
- Muthen, B. & Asparouhov, T. Bayesian structural equation modeling: a more flexible representation of substantive theory. Psychol. Methods17, 313–335 (2012). Google Scholar
- van de Schoot, R. et al. Facing off with Scylla and Charybdis: a comparison of scalar, partial, and the novel possibility of approximate measurement invariance. Front. Psychol.4, 770 (2013). Google Scholar
- Smeets, L. & van de Schoot, R. Code for the ShinyApp to determine the plausible parameter space for the PhD-delay data (version v1.0). Zenodohttps://doi.org/10.5281/zenodo.3999424 (2020). ArticleGoogle Scholar
- Chung, Y., Gelman, A., Rabe-Hesketh, S., Liu, J. & Dorie, V. Weakly informative prior for point estimation of covariance matrices in hierarchical models. J. Educ. Behav. Stat.40, 136–157 (2015). Google Scholar
- Gelman, A., Jakulin, A., Pittau, M. G. & Su, Y.-S. A weakly informative default prior distribution for logistic and other regression models. Ann. Appl. Stat.2, 1360–1383 (2008). MathSciNetMATHGoogle Scholar
- Gelman, A., Carlin, J. B., Stern, H. S. & Rubin, D. B. Bayesian Data Analysis Vol. 2 (Chapman&HallCRC, 2004).
- Jeffreys, H. Theory of Probability Vol. 3 (Clarendon, 1961).
- Seaman III, J. W., Seaman Jr, J. W. & Stamey, J. D. Hidden dangers of specifying noninformative priors. Am. Stat.66, 77–84 (2012). MathSciNetGoogle Scholar
- Gelman, A. Prior distributions for variance parameters in hierarchical models (comment on article by Browne and Draper). Bayesian Anal.1, 515–534 (2006). MathSciNetMATHGoogle Scholar
- Lambert, P. C., Sutton, A. J., Burton, P. R., Abrams, K. R. & Jones, D. R. How vague is vague? A simulation study of the impact of the use of vague prior distributions in MCMC using WinBUGS. Stat. Med.24, 2401–2428 (2005). MathSciNetGoogle Scholar
- Depaoli, S. Mixture class recovery in GMM under varying degrees of class separation: frequentist versus Bayesian estimation. Psychol. Methods18, 186–219 (2013). Google Scholar
- Depaoli, S. & van de Schoot, R. Improving transparency and replication in Bayesian statistics: the WAMBS-Checklist. Psychol. Methods22, 240 (2017). This article describes, in a step-by-step manner, the various points that need to be checked when estimating a model using Bayesian statistics. It can be used as a guide for implementing Bayesian methods. Google Scholar
- van Erp, S., Mulder, J. & Oberski, D. L. Prior sensitivity analysis in default Bayesian structural equation modeling. Psychol. Methods23, 363–388 (2018). Google Scholar
- McNeish, D. On using Bayesian methods to address small sample problems. Struct. Equ. Modeling23, 750–773 (2016). MathSciNetGoogle Scholar
- van de Schoot, R. & Miocević, M. Small Sample Size Solutions: A Guide for Applied Researchers and Practitioners (Taylor & Francis, 2020).
- Schuurman, N. K., Grasman, R. P. & Hamaker, E. L. A comparison of inverse-Wishart prior specifications for covariance matrices in multilevel autoregressive models. Multivariate Behav. Res.51, 185–206 (2016). Google Scholar
- Liu, H., Zhang, Z. & Grimm, K. J. Comparison of inverse Wishart and separation-strategy priors for Bayesian estimation of covariance parameter matrix in growth curve analysis. Struct. Equ. Modeling23, 354–367 (2016). MathSciNetGoogle Scholar
- Ranganath, R. & Blei, D. M. Population predictive checks. Preprint at https://arxiv.org/abs/1908.00882 (2019).
- Daimon, T. Predictive checking for Bayesian interim analyses in clinical trials. Contemp. Clin. Trials29, 740–750 (2008). Google Scholar
- Box, G. E. Sampling and Bayes’ inference in scientific modelling and robustness. J. R. Stat. Soc. Ser. A143, 383–404 (1980). MathSciNetMATHGoogle Scholar
- Gabry, J., Simpson, D., Vehtari, A., Betancourt, M. & Gelman, A. Visualization in Bayesian workflow. J. R. Stat. Soc. Ser. A182, 389–402 (2019). MathSciNetGoogle Scholar
- Silverman, B. W. Density Estimation for Statistics and Data Analysis Vol. 26 (CRC, 1986).
- Nott, D. J., Drovandi, C. C., Mengersen, K. & Evans, M. Approximation of Bayesian predictive p-values with regression ABC. Bayesian Anal.13, 59–83 (2018). MathSciNetMATHGoogle Scholar
- Evans, M. & Moshonov, H. in Bayesian Statistics and its Applications 145–159 (Univ. of Toronto, 2007).
- Evans, M. & Moshonov, H. Checking for prior–data conflict. Bayesian Anal.1, 893–914 (2006). MathSciNetMATHGoogle Scholar
- Evans, M. & Jang, G. H. A limit result for the prior predictive applied to checking for prior–data conflict. Stat. Probab. Lett.81, 1034–1038 (2011). MathSciNetMATHGoogle Scholar
- Young, K. & Pettit, L. Measuring discordancy between prior and data. J. R. Stat. Soc. Series B Methodol.58, 679–689 (1996). MathSciNetMATHGoogle Scholar
- Kass, R. E. & Raftery, A. E. Bayes factors. J. Am. Stat. Assoc.90, 773–795 (1995). This article provides an extensive discussion of Bayes factors with several examples. MathSciNetMATHGoogle Scholar
- Bousquet, N. Diagnostics of prior–data agreement in applied Bayesian analysis. J. Appl. Stat.35, 1011–1029 (2008). MathSciNetMATHGoogle Scholar
- Veen, D., Stoel, D., Schalken, N., Mulder, K. & van de Schoot, R. Using the data agreement criterion to rank experts’ beliefs. Entropy20, 592 (2018). ADSGoogle Scholar
- Nott, D. J., Xueou, W., Evans, M. & Englert, B. Checking for prior–data conflict using prior to posterior divergences. Preprint at https://arxiv.org/abs/1611.00113 (2016).
- Lek, K. & van de Schoot, R. How the choice of distance measure influences the detection of prior–data conflict. Entropy21, 446 (2019). ADSMathSciNetGoogle Scholar
- O’Hagan, A. Bayesian statistics: principles and benefits. Frontis3, 31–45 (2004). Google Scholar
- Etz, A. Introduction to the concept of likelihood and its applications. Adv. Methods Practices Psychol. Sci.1, 60–69 (2018). Google Scholar
- Pawitan, Y. In All Likelihood: Statistical Modelling and Inference Using Likelihood (Oxford Univ. Press, 2001).
- Gelman, A., Simpson, D. & Betancourt, M. The prior can often only be understood in the context of the likelihood. Entropy19, 555 (2017). ADSGoogle Scholar
- Aczel, B. et al. Discussion points for Bayesian inference. Nat. Hum. Behav.4, 561–563 (2020). Google Scholar
- Gelman, A. et al. Bayesian Data Analysis (CRC, 2013).
- Greco, L., Racugno, W. & Ventura, L. Robust likelihood functions in Bayesian inference. J. Stat. Plan. Inference138, 1258–1270 (2008). MathSciNetMATHGoogle Scholar
- Shyamalkumar, N. D. in Robust Bayesian Analysis Lecture Notes in Statistics Ch. 7, 127–143 (Springer, 2000).
- Agostinelli, C. & Greco, L. A weighted strategy to handle likelihood uncertainty in Bayesian inference. Comput. Stat.28, 319–339 (2013). MathSciNetMATHGoogle Scholar
- Rubin, D. B. Bayesianly justifiable and relevant frequency calculations for the applied statistician. Ann. Stat.12, 1151–1172 (1984). MathSciNetMATHGoogle Scholar
- Gelfand, A. E. & Smith, A. F. M. Sampling-based approaches to calculating marginal densities. J. Am. Stat. Assoc.85, 398–409 (1990). This seminal article identifies MCMC as a practical approach for Bayesian inference. MathSciNetMATHGoogle Scholar
- Geyer, C. J. Markov chain Monte Carlo maximum likelihood. IFNAhttp://hdl.handle.net/11299/58440 (1991).
- van de Schoot, R., Veen, D., Smeets, L., Winter, S. D. & Depaoli, S. in Small Sample Size Solutions: A Guide for Applied Researchers and Practitioners Ch. 3 (eds van de Schoot, R. & Miocevic, M.) 30–49 (Routledge, 2020).
- Veen, D. & Egberts, M. in Small Sample Size Solutions: A Guide for Applied Researchers and Practitioners Ch. 4 (eds van de Schoot, R. & Miocevic, M.) 50–70 (Routledge, 2020).
- Robert, C. & Casella, G. Monte Carlo Statistical Methods (Springer Science & Business Media, 2013).
- Geman, S. & Geman, D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Trans. Pattern Anal. Mach. Intell.6, 721–741 (1984). MATHGoogle Scholar
- Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H. & Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys.21, 1087–1092 (1953). ADSMATHGoogle Scholar
- Hastings, W. K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika57, 97–109 (1970). MathSciNetMATHGoogle Scholar
- Duane, S., Kennedy, A. D., Pendleton, B. J. & Roweth, D. Hybrid Monte Carlo. Phys. Lett. B195, 216–222 (1987). ADSMathSciNetGoogle Scholar
- Tanner, M. A. & Wong, W. H. The calculation of posterior distributions by data augmentation. J. Am. Stat. Assoc.82, 528–540 (1987). This article explains how to use data augmentation when direct computation of the posterior density of the parameters of interest is not possible. MathSciNetMATHGoogle Scholar
- Gamerman, D. & Lopes, H. F. Markov Chain Monte Carlo: Stochastic Simulation for Bayesian Inference (CRC, 2006).
- Brooks, S. P., Gelman, A., Jones, G. & Meng, X.-L. Handbook of Markov Chain Monte Carlo (CRC, 2011). This book presents a comprehensive review of MCMC and its use in many different applications.
- Gelman, A. Burn-in for MCMC, why we prefer the term warm-up. Satistical Modeling, Causal Inference, and Social Sciencehttps://statmodeling.stat.columbia.edu/2017/12/15/burn-vs-warm-iterative-simulation-algorithms/ (2017).
- Gelman, A. & Rubin, D. B. Inference from iterative simulation using multiple sequences. Stat. Sci.7, 457–511 (1992). MATHGoogle Scholar
- Brooks, S. P. & Gelman, A. General methods for monitoring convergence of iterative simulations. J. Comput. Graph. Stat.7, 434–455 (1998). MathSciNetGoogle Scholar
- Roberts, G. O. Markov chain concepts related to sampling algorithms. Markov Chain Monte Carlo in Practice57, 45–58 (1996). MathSciNetMATHGoogle Scholar
- Vehtari, A., Gelman, A., Simpson, D., Carpenter, B. & Bürkner, P. Rank-normalization, folding, and localization: an improved \(\hat\) for assessing convergence of MCMC. Preprint at https://arxiv.org/abs/1903.08008 (2020).
- Bürkner, P.-C. Advanced Bayesian multilevel modeling with the R package brms. Preprint at https://arxiv.org/abs/1705.11123 (2017).
- Merkle, E. C. & Rosseel, Y. blavaan: Bayesian structural equation models via parameter expansion. Preprint at https://arxiv.org/abs/1511.05604 (2015).
- Carpenter, B. et al. Stan: a probabilistic programming language. J. Stat. Softw.https://doi.org/10.18637/jss.v076.i01 (2017). ArticleGoogle Scholar
- Blei, D. M., Kucukelbir, A. & McAuliffe, J. D. Variational inference: a review for statisticians. J. Am. Stat. Assoc.112, 859–877 (2017). This recent review of variational inference methods includes stochastic variants that underpin popular approximate Bayesian inference methods for large data or complex modelling problems. MathSciNetGoogle Scholar
- Minka, T. P. Expectation propagation for approximate Bayesian inference. Preprint at https://arxiv.org/abs/1301.2294 (2013).
- Hoffman, M. D., Blei, D. M., Wang, C. & Paisley, J. Stochastic variational inference. J. Mach. Learn. Res.14, 1303–1347 (2013). MathSciNetMATHGoogle Scholar
- Kingma, D. P. & Ba, J. Adam: a method for stochastic optimization. Preprint at https://arxiv.org/abs/1412.6980 (2014).
- Li, Y., Hernández-Lobato, J. M. & Turner, R. E. Stochastic expectation propagation. Adv. Neural Inf. Process. Syst.28, 2323–2331 (2015). Google Scholar
- Liang, F., Paulo, R., Molina, G., Clyde, M. A. & Berger, J. O. Mixtures of g priors for Bayesian variable selection. J. Am. Stat. Assoc.103, 410–423 (2008). MathSciNetMATHGoogle Scholar
- Forte, A., Garcia-Donato, G. & Steel, M. Methods and tools for Bayesian variable selection and model averaging in normal linear regression. Int. Stat.Rev.86, 237–258 (2018). MathSciNetGoogle Scholar
- Mitchell, T. J. & Beauchamp, J. J. Bayesian variable selection in linear regression. J. Am. Stat. Assoc.83, 1023–1032 (1988). MathSciNetMATHGoogle Scholar
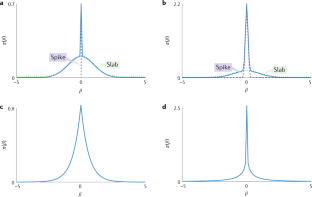
- George, E. J. & McCulloch, R. E. Variable selection via Gibbs sampling. J. Am. Stat. Assoc.88, 881–889 (1993). This article popularizes the use of spike-and-slab priors for Bayesian variable selection and introduces MCMC techniques to explore the model space. Google Scholar
- Ishwaran, H. & Rao, J. S. Spike and slab variable selection: frequentist and Bayesian strategies. Ann. Stat.33, 730–773 (2005). MathSciNetMATHGoogle Scholar
- Bottolo, L. & Richardson, S. Evolutionary stochastic search for Bayesian model exploration. Bayesian Anal.5, 583–618 (2010). MathSciNetMATHGoogle Scholar
- Ročková, V. & George, E. I. EMVS: the EM approach to Bayesian variable selection. J. Am. Stat. Assoc.109, 828–846 (2014). MathSciNetMATHGoogle Scholar
- Park, T. & Casella, G. The Bayesian lasso. J. Am. Stat. Assoc.103, 681–686 (2008). MathSciNetMATHGoogle Scholar
- Carvalho, C. M., Polson, N. G. & Scott, J. G. The horseshoe estimator for sparse signals. Biometrika97, 465–480 (2010). MathSciNetMATHGoogle Scholar
- Polson, N. G. & Scott, J. G. Shrink globally, act locally: sparse Bayesian regularization and prediction. Bayesian Stat.9, 105 (2010). This article provides a unified framework for continuous shrinkage priors, which allow global sparsity while controlling the amount of regularization for each regression coefficient. Google Scholar
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Series B58, 267–288 (1996). MathSciNetMATHGoogle Scholar
- Van Erp, S., Oberski, D. L. & Mulder, J. Shrinkage priors for Bayesian penalized regression. J. Math. Psychol.89, 31–50 (2019). MathSciNetMATHGoogle Scholar
- Brown, P. J., Vannucci, M. & Fearn, T. Multivariate Bayesian variable selection and prediction. J. R. Stat. Soc. Series B60, 627–641 (1998). MathSciNetMATHGoogle Scholar
- Lee, K. H., Tadesse, M. G., Baccarelli, A. A., Schwartz, J. & Coull, B. A. Multivariate Bayesian variable selection exploiting dependence structure among outcomes: application to air pollution effects on DNA methylation. Biometrics73, 232–241 (2017). MathSciNetMATHGoogle Scholar
- Frühwirth-Schnatter, S. & Wagner, H. Stochastic model specification search for Gaussian and partially non-Gaussian state space models. J. Econom.154, 85–100 (2010). MATHGoogle Scholar
- Scheipl, F., Fahrmeir, L. & Kneib, T. Spike-and-slab priors for function selection in structured additive regression models. J. Am. Stat. Assoc.107, 1518–1532 (2012). MathSciNetMATHGoogle Scholar
- Tadesse, M. G., Sha, N. & Vannucci, M. Bayesian variable selection in clustering high dimensional data. J. Am. Stat. Assoc.https://doi.org/10.1198/016214504000001565 (2005). ArticleMathSciNetMATHGoogle Scholar
- Wang, H. Scaling it up: stochastic search structure learning in graphical models. Bayesian Anal.10, 351–377 (2015). MathSciNetMATHGoogle Scholar
- Peterson, C. B., Stingo, F. C. & Vannucci, M. Bayesian inference of multiple Gaussian graphical models. J. Am. Stat. Assoc.110, 159–174 (2015). MathSciNetMATHGoogle Scholar
- Li, F. & Zhang, N. R. Bayesian variable selection in structured high-dimensional covariate spaces with applications in genomics. J. Am. Stat. Assoc.105, 1978–2002 (2010). MathSciNetGoogle Scholar
- Stingo, F., Chen, Y., Tadesse, M. G. & Vannucci, M. Incorporating biological information into linear models: a Bayesian approach to the selection of pathways and genes. Ann. Appl. Stat.5, 1202–1214 (2011). MathSciNetMATHGoogle Scholar
- Guan, Y. & Stephens, M. Bayesian variable selection regression for genome-wide association studies and other large-scale problems. Ann. Appl. Stat.5, 1780–1815 (2011). MathSciNetMATHGoogle Scholar
- Bottolo, L. et al. GUESS-ing polygenic associations with multiple phenotypes using a GPU-based evolutionary stochastic search algorithm. PLoS Genetics9, e1003657–e1003657 (2013). Google Scholar
- Banerjee, S., Carlin, B. P. & Gelfand, A. E. Hierarchical Modeling and Analysis for Spatial Data (CRC, 2014).
- Vock, L. F. B., Reich, B. J., Fuentes, M. & Dominici, F. Spatial variable selection methods for investigating acute health effects of fine particulate matter components. Biometrics71, 167–177 (2015). MathSciNetMATHGoogle Scholar
- Penny, W. D., Trujillo-Barreto, N. J. & Friston, K. J. Bayesian fMRI time series analysis with spatial priors. Neuroimage24, 350–362 (2005). Google Scholar
- Smith, M., Pütz, B., Auer, D. & Fahrmeir, L. Assessing brain activity through spatial Bayesian variable selection. Neuroimage20, 802–815 (2003). Google Scholar
- Zhang, L., Guindani, M., Versace, F. & Vannucci, M. A spatio-temporal nonparametric Bayesian variable selection model of fMRI data for clustering correlated time courses. Neuroimage95, 162–175 (2014). Google Scholar
- Gorrostieta, C., Fiecas, M., Ombao, H., Burke, E. & Cramer, S. Hierarchical vector auto-regressive models and their applications to multi-subject effective connectivity. Front. Computat. Neurosci.7, 159–159 (2013). Google Scholar
- Chiang, S. et al. Bayesian vector autoregressive model for multi-subject effective connectivity inference using multi-modal neuroimaging data. Human Brain Mapping38, 1311–1332 (2017). Google Scholar
- Schad, D. J., Betancourt, M. & Vasishth, S. Toward a principled Bayesian workflow in cognitive science. Preprint at https://arxiv.org/abs/1904.12765 (2019).
- Gelman, A., Meng, X.-L. & Stern, H. Posterior predictive assessment of model fitness via realized discrepancies. Stat. Sinica6, 733–760 (1996). MathSciNetMATHGoogle Scholar
- Meng, X.-L. Posterior predictive p-values. Ann. Stat.22, 1142–1160 (1994). MathSciNetMATHGoogle Scholar
- Asparouhov, T., Hamaker, E. L. & Muthén, B. Dynamic structural equation models. Struct. Equ. Modeling25, 359–388 (2018). MathSciNetGoogle Scholar
- Zhang, Z., Hamaker, E. L. & Nesselroade, J. R. Comparisons of four methods for estimating a dynamic factor model. Struct. Equ. Modeling15, 377–402 (2008). MathSciNetGoogle Scholar
- Hamaker, E., Ceulemans, E., Grasman, R. & Tuerlinckx, F. Modeling affect dynamics: state of the art and future challenges. Emot. Rev.7, 316–322 (2015). Google Scholar
- Meissner, P. wikipediatrend: Public Subject Attention via Wikipedia Page View Statistics. R package version 2.1.6. Peter Meissnerhttps://CRAN.R-project.org/package=wikipediatrend (2020).
- Veen, D. & van de Schoot, R. Bayesian analysis for PhD-delay dataset. OSFhttps://doi.org/10.17605/OSF.IO/JA859 (2020). ArticleGoogle Scholar
- Harvey, A. C. & Peters, S. Estimation procedures for structural time series models. J. Forecast.9, 89–108 (1990). Google Scholar
- Taylor, S. J. & Letham, B. Forecasting at scale. Am. Stat.72, 37–45 (2018). MathSciNetGoogle Scholar
- Gopnik, A. & Bonawitz, E. Bayesian models of child development. Wiley Interdiscip. Rev. Cogn. Sci.6, 75–86 (2015). Google Scholar
- Gigerenzer, G. & Hoffrage, U. How to improve Bayesian reasoning without instruction: frequency formats. Psychol. Rev.102, 684 (1995). Google Scholar
- Slovic, P. & Lichtenstein, S. Comparison of Bayesian and regression approaches to the study of information processing in judgment. Organ. Behav. Hum. Perform.6, 649–744 (1971). Google Scholar
- Bolt, D. M., Piper, M. E., Theobald, W. E. & Baker, T. B. Why two smoking cessation agents work better than one: role of craving suppression. J. Consult. Clin. Psychol.80, 54–65 (2012). Google Scholar
- Billari, F. C., Graziani, R. & Melilli, E. Stochastic population forecasting based on combinations of expert evaluations within the Bayesian paradigm. Demography51, 1933–1954 (2014). Google Scholar
- Fallesen, P. & Breen, R. Temporary life changes and the timing of divorce. Demography53, 1377–1398 (2016). Google Scholar
- Hansford, T. G., Depaoli, S. & Canelo, K. S. Locating U.S. Solicitors General in the Supreme Court’s policy space. Pres. Stud. Q.49, 855–869 (2019). Google Scholar
- Phipps, D. J., Hagger, M. S. & Hamilton, K. Predicting limiting ‘free sugar’ consumption using an integrated model of health behavior. Appetite150, 104668 (2020). Google Scholar
- Depaoli, S., Rus, H. M., Clifton, J. P., van de Schoot, R. & Tiemensma, J. An introduction to Bayesian statistics in health psychology. Health Psychol. Rev.11, 248–264 (2017). Google Scholar
- Kruschke, J. K. Bayesian estimation supersedes the t test. J. Exp. Psychol. Gen.142, 573–603 (2013). Google Scholar
- Lee, M. D. How cognitive modeling can benefit from hierarchical Bayesian models. J. Math. Psychol.55, 1–7 (2011). MathSciNetMATHGoogle Scholar
- Royle, J. & Dorazio, R. Hierarchical Modeling and Inference in Ecology (Academic, 2008).
- Gimenez, O. et al. in Modeling Demographic Processes in Marked Populations Vol. 3 (eds Thomson D. L., Cooch E. G. & Conroy M. J.) 883–915 (Springer, 2009).
- King, R., Morgan, B., Gimenez, O. & Brooks, S. P. Bayesian Analysis for Population Ecology (CRC, 2009).
- Kéry, M. & Schaub, M. Bayesian Population Analysis using WinBUGS: A Hierarchical Perspective (Academic, 2011).
- McCarthy, M. Bayesian Methods of Ecology 5th edn (Cambridge Univ. Press, 2012).
- Korner-Nievergelt, F. et al. Bayesian Data Analysis in Ecology Using Linear Models with R, BUGS, and Stan (Academic, 2015).
- Monnahan, C. C., Thorson, J. T. & Branch, T. A. Faster estimation of Bayesian models in ecology using Hamiltonian Monte Carlo. Methods Ecol. Evol.8, 339–348 (2017). Google Scholar
- Ellison, A. M. Bayesian inference in ecology. Ecol. Lett.7, 509–520 (2004). Google Scholar
- Choy, S. L., O’Leary, R. & Mengersen, K. Elicitation by design in ecology: using expert opinion to inform priors for Bayesian statistical models. Ecology90, 265–277 (2009). Google Scholar
- Kuhnert, P. M., Martin, T. G. & Griffiths, S. P. A guide to eliciting and using expert knowledge in Bayesian ecological models. Ecol. Lett.13, 900–914 (2010). Google Scholar
- King, R., Brooks, S. P., Mazzetta, C., Freeman, S. N. & Morgan, B. J. Identifying and diagnosing population declines: a Bayesian assessment of lapwings in the UK. J. R. Stat. Soc. Series C57, 609–632 (2008). MathSciNetGoogle Scholar
- Newman, K. et al. Modelling Population Dynamics (Springer, 2014).
- Bachl, F. E., Lindgren, F., Borchers, D. L. & Illian, J. B. inlabru: an R package for Bayesian spatial modelling from ecological survey data. Methods Ecol. Evol.10, 760–766 (2019). Google Scholar
- King, R. & Brooks, S. P. On the Bayesian estimation of a closed population size in the presence of heterogeneity and model uncertainty. Biometrics64, 816–824 (2008). MathSciNetMATHGoogle Scholar
- Saunders, S. P., Cuthbert, F. J. & Zipkin, E. F. Evaluating population viability and efficacy of conservation management using integrated population models. J. Appl. Ecol.55, 1380–1392 (2018). Google Scholar
- McClintock, B. T. et al. A general discrete-time modeling framework for animal movement using multistate random walks. Ecol. Monog.82, 335–349 (2012). Google Scholar
- Dennis, B., Ponciano, J. M., Lele, S. R., Taper, M. L. & Staples, D. F. Estimating density dependence, process noise, and observation error. Ecol. Monog.76, 323–341 (2006). Google Scholar
- Aeberhard, W. H., Mills Flemming, J. & Nielsen, A. Review of state-space models for fisheries science. Ann. Rev. Stat. Appl.5, 215–235 (2018). Google Scholar
- Isaac, N. J. B. et al. Data integration for large-scale models of species distributions. Trends Ecol Evol35, 56–67 (2020). Google Scholar
- McClintock, B. T. et al. Uncovering ecological state dynamics with hidden Markov models. Preprint at https://arxiv.org/abs/2002.10497 (2020).
- King, R. Statistical ecology. Ann. Rev. Stat. Appl.1, 401–426 (2014). Google Scholar
- Fearnhead, P. in Handbook of Markov Chain Monte Carlo Ch. 21 (eds Brooks, S., Gelman, A., Jones, G.L. & Meng, X.L.) 513–529 (Chapman & Hall/CRC, 2011).
- Andrieu, C., Doucet, A. & Holenstein, R. Particle Markov chain Monte Carlo methods. J. R. Stat. Soc. Series B72, 269–342 (2010). MathSciNetMATHGoogle Scholar
- Knape, J. & de Valpine, P. Fitting complex population models by combining particle filters with Markov chain Monte Carlo. Ecology93, 256–263 (2012). Google Scholar
- Finke, A., King, R., Beskos, A. & Dellaportas, P. Efficient sequential Monte Carlo algorithms for integrated population models. J. Agric. Biol. Environ. Stat.24, 204–224 (2019). MathSciNetMATHGoogle Scholar
- Stephens, M. & Balding, D. J. Bayesian statistical methods for genetic association studies. Nat. Rev. Genet10, 681–690 (2009). Google Scholar
- Mimno, D., Blei, D. M. & Engelhardt, B. E. Posterior predictive checks to quantify lack-of-fit in admixture models of latent population structure. Proc. Natl Acad. Sci. USA112, E3441–3450 (2015). ADSGoogle Scholar
- Schaid, D. J., Chen, W. & Larson, N. B. From genome-wide associations to candidate causal variants by statistical fine-mapping. Nat. Rev. Genet.19, 491–504 (2018). Google Scholar
- Marchini, J. & Howie, B. Genotype imputation for genome-wide association studies. Nat. Rev. Genet.11, 499–511 (2010). Google Scholar
- Allen, N. E., Sudlow, C., Peakman, T., Collins, R. & Biobank, U. K. UK Biobank data: come and get it. Sci. Transl. Med.6, 224ed224 (2014). Google Scholar
- Cortes, A. et al. Bayesian analysis of genetic association across tree-structured routine healthcare data in the UK Biobank. Nat. Genet.49, 1311–1318 (2017). Google Scholar
- Argelaguet, R. et al. Multi-omics factor analysis — a framework for unsupervised integration of multi-omics data sets. Mol. Syst. Biol.14, e8124 (2018). Google Scholar
- Stuart, T. & Satija, R. Integrative single-cell analysis. Nat. Rev. Genet.20, 257–272 (2019). Google Scholar
- Yau, C. & Campbell, K. Bayesian statistical learning for big data biology. Biophys. Rev.11, 95–102 (2019). Google Scholar
- Vallejos, C. A., Marioni, J. C. & Richardson, S. BASiCS: Bayesian analysis of single-cell sequencing data. PLoS Comput. Biol.11, e1004333 (2015). ADSGoogle Scholar
- Wang, J. et al. Data denoising with transfer learning in single-cell transcriptomics. Nat. Methods16, 875–878 (2019). Google Scholar
- Lopez, R., Regier, J., Cole, M. B., Jordan, M. I. & Yosef, N. Deep generative modeling for single-cell transcriptomics. Nat. Methods15, 1053–1058 (2018). Google Scholar
- National Cancer Institute. The Cancer Genome Atlas. Qeioshttps://doi.org/10.32388/e1plqh (2020).
- Kuipers, J. et al. Mutational interactions define novel cancer subgroups. Nat. Commun.9, 4353 (2018). ADSGoogle Scholar
- Schwartz, R. & Schaffer, A. A. The evolution of tumour phylogenetics: principles and practice. Nat. Rev. Genet.18, 213–229 (2017). Google Scholar
- Munafò, M. R. et al. A manifesto for reproducible science. Nat. Hum. Behav.https://doi.org/10.1038/s41562-016-0021 (2017). ArticleGoogle Scholar
- Wilkinson, M. D. et al. The FAIR guiding principles for scientific data management and stewardship. Sci. Data3, 160018 (2016). Google Scholar
- Lamprecht, A.-L. et al. Towards FAIR principles for research software. Data Sci.3, 37–59 (2020). Google Scholar
- Smith, A. M., Katz, D. S. & Niemeyer, K. E. Software citation principles. PeerJ Comput. Sci.2, e86 (2016). Google Scholar
- Clyburne-Sherin, A., Fei, X. & Green, S. A. Computational reproducibility via containers in psychology. Meta Psychol.https://doi.org/10.15626/MP.2018.892 (2019). ArticleGoogle Scholar
- Lowenberg, D. Dryad & Zenodo: our path ahead. WordPresshttps://blog.datadryad.org/2020/03/10/dryad-zenodo-our-path-ahead/ (2020).
- Nosek, B. A. et al. Promoting an open research culture. Science348, 1422–1425 (2015). ADSGoogle Scholar
- Vehtari, A. & Ojanen, J. A survey of Bayesian predictive methods for model assessment, selection and comparison. Stat. Surv.6, 142–228 (2012). MathSciNetMATHGoogle Scholar
- Abadi, M. et al. in USENIX Symposium on Operating Systems Design and Implementation (OSDI'16) 265–283 (USENIX Association, 2016).
- Paszke, A. et al. in Advances in Neural Information Processing Systems (eds Wallach, H. et al.) 8026–8037 (Urran Associates, 2019).
- Kingma, D. P. & Welling, M. An introduction to variational autoencoders. Preprint at https://arxiv.org/abs/1906.02691 (2019). This recent review of variational autoencoders encompasses deep generative models, the re-parameterization trick and current inference methods.
- Higgins, I. et al. beta-VAE: learning basic visual concepts with a constrained variational framework. ICLR 2017https://openreview.net/forum?id=Sy2fzU9gl (2017).
- Märtens, K. & Yau, C. BasisVAE:tTranslation-invariant feature-level clustering with variational autoencoders. Preprint at https://arxiv.org/abs/2003.03462 (2020).
- Liu, Q., Allamanis, M., Brockschmidt, M. & Gaunt, A. in Advances in Neural Information Processing Systems 31 (eds Bengio, S. et al.) 7795–7804 (Curran Associates, 2018).
- Louizos, C., Shi, X., Schutte, K. & Welling, M. in Advances in Neural Information Processing Systems 8743-8754 (MIT Press, 2019).
- Garnelo, M. et al. in Proceedings of the 35th International Conference on Machine Learning Vol. 80 (eds Dy, J. & Krause, A.) 1704–1713 (PMLR, 2018).
- Kim, H. et al. Attentive neural processes. Preprint at https://arxiv.org/abs/1901.05761 (2019).
- Rezende, D. & Mohamed, S. in Proceedings of the 32nd International Conference on Machine Learning Vol. 37 (eds Bach, F. & Blei, D.) 1530–1538 (PMLR, 2015).
- Papamakarios, G., Nalisnick, E., Rezende, D. J., Mohamed, S. & Lakshminarayanan, B. Normalizing flows for probabilistic modeling and inference. Preprint at https://arxiv.org/abs/1912.02762 (2019).
- Korshunova, I. et al. in Advances in Neural Information Processing Systems 31 (eds Bengio, S.et al.) 7190–7198 (Curran Associates, 2018).
- Zhang, R., Li, C., Zhang, J., Chen, C. & Wilson, A. G. Cyclical stochastic gradient MCMC for Bayesian deep learning. Preprint at https://arxiv.org/abs/1902.03932 (2019).
- Neal, R. M. Bayesian Learning for Neural Networks (Springer Science & Business Media, 2012).
- Neal, R. M. in Bayesian Learning for Neural Networks Lecture Notes in Statistics Ch 2 (ed Nea, R. M.) 29–53 (Springer, 1996). This classic text highlights the connection between neural networks and Gaussian processes and the application of Bayesian approaches for fitting neural networks.
- Williams, C. K. I. in Advances in Neural Information Processing Systems 295–301 (MIT Press, 1997).
- MacKay David, J. C. A practical Bayesian framework for backprop networks. Neural. Comput.https://doi.org/10.1162/neco.1992.4.3.448 (1992). ArticleGoogle Scholar
- Sun, S., Zhang, G., Shi, J. & Grosse, R. Functional variational Bayesian neural networks. Preprint at https://arxiv.org/abs/1903.05779 (2019).
- Lakshminarayanan, B., Pritzel, A. & Blundell, C. Simple and scalable predictive uncertainty estimation using deep ensembles. Advances in Neural Information Processing Systems30, 6402–6413 (2017). Google Scholar
- Wilson, A. G. The case for Bayesian deep learning. Preprint at https://arxiv.org/abs/2001.10995 (2020).
- Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I. & Salakhutdinov, R. Dropout: a simple way to prevent neural networks from overfitting. J. Mach. Learn. Res.15, 1929–1958 (2014). MathSciNetMATHGoogle Scholar
- Gal, Y. & Ghahramani, Z. in International Conference on Machine Learning 1050–1059 (JMLR, 2016).
- Green, P. J. Reversible jump Markov chain Monte Carlo computation and Bayesian model determination. Biometrika82, 711–732 (1995). MathSciNetMATHGoogle Scholar
- Hoffman, M. D. & Gelman, A. The No-U-Turn Sampler: adaptively setting path lengths in Hamiltonian Monte Carlo. J. Mach. Learn. Res.15, 1593–1623 (2014). MathSciNetMATHGoogle Scholar
- Liang, F. & Wong, W. H. Evolutionary Monte Carlo: applications to Cp model sampling and change point problem. Stat. Sinica 317-342 (2000).
- Liu, J. S. & Chen, R. Sequential Monte Carlo methods for dynamic systems. J. Am. Stat. Assoc.93, 1032–1044 (1998). MathSciNetMATHGoogle Scholar
- Sisson, S., Fan, Y. & Beaumont, M. Handbook of Approximate Bayesian Computation (Chapman and Hall/CRC 2018).
- Rue, H., Martino, S. & Chopin, N. Approximate Bayesian inference for latent Gaussian models by using integrated nested Laplace approximations. J. R. Stat. Soc. Series B71, 319–392 (2009). MathSciNetMATHGoogle Scholar
- Lunn, D. J., Thomas, A., Best, N. & Spiegelhalter, D. WinBUGS — a Bayesian modelling framework: concepts, structure, and extensibility. Stat. Comput.10, 325–337 (2000). Google Scholar
- Ntzoufras, I. Bayesian Modeling Using WinBUGS Vol. 698 (Wiley, 2011).
- Lunn, D. J., Thomas, A., Best, N. & Spiegelhalter, D. WinBUGS — a Bayesian modelling framework: concepts, structure, and extensibility. Stat. Comput.10, 325–337 (2000). This paper provides an early user-friendly and freely available black-box MCMC sampler, opening up Bayesian inference to the wider scientific community. Google Scholar
- Spiegelhalter, D., Thomas, A., Best, N. & Lunn, D. OpenBUGS User Manual version 3.2.3. Openbugshttp://www.openbugs.net/w/Manuals?action=AttachFile&do=view&target=OpenBUGS_Manual.pdf (2014).
- Plummer, M. JAGS: a program for analysis of Bayesian graphical models using Gibbs sampling. Proc. 3rd International Workshop on Distributed Statistical Computing124, 1–10 (2003). Google Scholar
- Plummer, M. rjags: Bayesian graphical models using MCMC. R package version, 4(6) (2016).
- Salvatier, J., Wiecki, T. V. & Fonnesbeck, C. Probabilistic programming in Python using PyMC3. PeerJ Comput. Sci.2, e55 (2016). Google Scholar
- de Valpine, P. et al. Programming with models: writing statistical algorithms for general model structures with NIMBLE. J. Comput. Graph. Stat.s26, 403–413 (2017). MathSciNetGoogle Scholar
- Dillon, J. V. et al. Tensorflow distributions. Preprint at https://arxiv.org/abs/1711.10604 (2017).
- Keydana, S. tfprobability: R interface to TensorFlow probability. githubhttps://rstudio.github.io/tfprobability/index.html (2020).
- Bingham, E. et al. Pyro: deep universal probabilistic programming. J. Mach. Learn. Res.20, 973–978 (2019). MATHGoogle Scholar
- Bezanson, J., Karpinski, S., Shah, V. B. & Edelman, A. Julia: a fast dynamic language for technical computing. Preprint at https://arxiv.org/abs/1209.5145 (2012).
- Ge, H., Xu, K. & Ghahramani, Z. Turing: a language for flexible probabilistic inference. Proceedings of Machine Learning Research84, 1682–1690 (2018). Google Scholar
- Smith, B. J. et al. brian-j-smith/Mamba.jl: v0.12.4. Zenodohttps://doi.org/10.5281/zenodo.3740216 (2020).
- JASP Team. JASP (version 0.14) [computer software] (2020).
- Lindgren, F. & Rue, H. Bayesian spatial modelling with R-INLA. J. Stat. Soft.63, 1–25 (2015). Google Scholar
- Vanhatalo, J. et al. GPstuff: Bayesian modeling with Gaussian processes. J. Mach. Learn. Res.14, 1175–1179 (2013). MathSciNetMATHGoogle Scholar
- Blaxter, L. How to Research (McGraw-Hill Education, 2010).
- Neuman, W. L. Understanding Research (Pearson, 2016).
- Betancourt, M. Towards a principled Bayesian workflow. githubhttps://betanalpha.github.io/assets/case_studies/principled_bayesian_workflow.html (2020).
- Veen, D. & van de Schoot, R. Posterior predictive checks for the Premier League. OSFhttps://doi.org/10.17605/OSF.IO/7YRUD (2020). ArticleGoogle Scholar
- Kramer, B. & Bosman, J. Summerschool open science and scholarship 2019 — Utrecht University. ZENODOhttps://doi.org/10.5281/ZENODO.3925004 (2020). ArticleGoogle Scholar
- Rényi, A. On a new axiomatic theory of probability. Acta Math. Hung.6, 285–335 (1955). MathSciNetMATHGoogle Scholar
- Lesaffre, E. & Lawson, A. B. Bayesian Biostatistics (Wiley, 2012).
- Hoijtink, H., Beland, S. & Vermeulen, J. A. Cognitive diagnostic assessment via Bayesian evaluation of informative diagnostic hypotheses. Psychol Methods19, 21–38 (2014). Google Scholar
Acknowledgements
R.v.d.S. was supported by grant NWO-VIDI-452-14-006 from the Netherlands Organization for Scientific Research. R.K. was supported by Leverhulme research fellowship grant reference RF-2019-299 and by The Alan Turing Institute under the EPSRC grant EP/N510129/1. K.M. was supported by a UK Engineering and Physical Sciences Research Council Doctoral Studentship. C.Y. is supported by a UK Medical Research Council Research Grant (Ref. MR/P02646X/1) and by The Alan Turing Institute under the EPSRC grant EP/N510129/1











